Stack
A stack is an Abstract Data Type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example – a deck of cards or a pile of plates
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.
stack follows first-in-last-out methodology.
Basic Operations
Stack operations may involve initializing the stack, using it and then de-initializing it. Apart from these basic stuffs, a stack is used for the following two primary operations −
-
push() − Pushing (storing) an element on the stack.
-
pop() − Removing (accessing) an element from the stack.
When data is PUSHed onto stack.
To use a stack efficiently, we need to check the status of stack as well. For the same purpose, the following functionality is added to stacks −
-
peek() − get the top data element of the stack, without removing it.
-
isFull() − check if stack is full.
-
isEmpty() − check if stack is empty.
At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The top pointer provides top value of the stack without actually removing it.
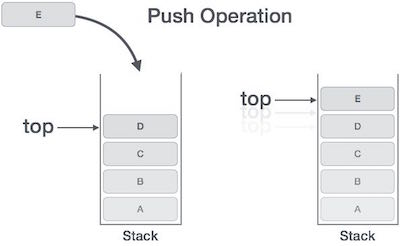
Push Operation
The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps −
-
Step 1 − Checks if the stack is full.
-
Step 2 − If the stack is full, produces an error and exit.
-
Step 3 − If the stack is not full, increments top to point next empty space.
-
Step 4 − Adds data element to the stack location, where top is pointing.
-
Step 5 − Returns success.
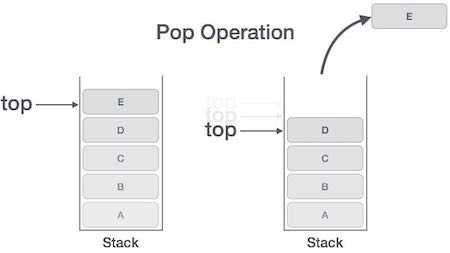
Pop Operation
A Pop operation may involve the following steps −
-
Step 1 − Checks if the stack is empty.
-
Step 2 − If the stack is empty, produces an error and exit.
-
Step 3 − If the stack is not empty, accesses the data element at which top is pointing.
-
Step 4 − Decreases the value of top by 1.
-
Step 5 − Returns success.
AS example for stack app we can look at Expression Parsing program that uses app but first let’s know more about notation :)
Expression Parsing
The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are −
- Infix Notation
- Prefix (Polish) Notation
- Postfix (Reverse-Polish) Notation
Infix Notation
We write expression in infix notation, e.g. a - b + c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption.
Prefix Notation
In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.
Postfix Notation
This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.
| Serial No. | Infix Notation | Prefix Notation | Postfix Notation |
|---|---|---|---|
| 1 | a + b | + a b | a b + |
| 2 | (a + b) ∗ c | ∗ + a b c | a b + c ∗ |
| 3 | a ∗ (b + c) | ∗ a + b c | a b c + ∗ |
| 4 | a / b + c / d | + / a b / c d | a b / c d / + |
| 5 | (a + b) ∗ (c + d) | ∗ + a b + c d | a b + c d + ∗ |
| 6 | ((a + b) ∗ c) - d | - ∗ + a b c d | a b + c ∗ d - |