Binary Search

Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in the sorted form.

How Binary Search Works?

1. starting from ordered lists.

   

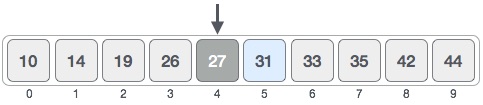
2. identify mid index of the array with this equation mid = low + (high - low) / 2 which is 0 + (9 - 0 ) / 2 = 4
   

3. Now we compare the value stored at location 4, with the value being searched (31),We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

4. We change our low to mid + 1 and find the new mid value again. \(low = mid + 1, mid =low + \frac{(high - low)}{2}\) Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.

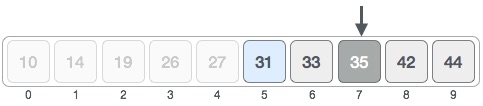
   The value stored at location 7 is not a match, rather it is more than what we are looking for. So, the value must be in the lower part from this location.

5. Hence, we calculate the mid again. This time it is 5. 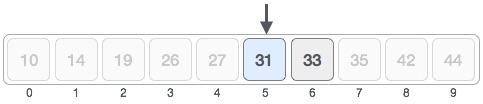We compare the value stored at location 5 with our target value. We find that it is a match.

Time Complexity = Ο(log n)
Space Complexity = O(3)