Binary Search Tree
Tree represents the nodes connected by edges.
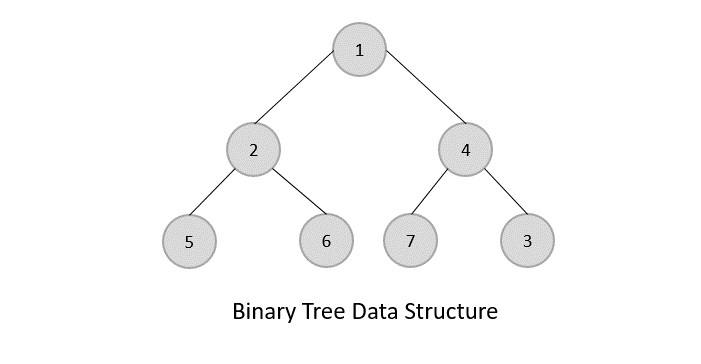
Important Terms
Following are the important terms with respect to tree.
-
Path − Path refers to the sequence of nodes along the edges of a tree.
-
Root − The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
-
Parent − Any node except the root node has one edge upward to a node called parent.
-
Child − The node below a given node connected by its edge downward is called its child node.
-
Leaf − The node which does not have any child node is called the leaf node.
-
Subtree − Subtree represents the descendants of a node.
-
Visiting − Visiting refers to checking the value of a node when control is on the node.
-
Traversing − Traversing means passing through nodes in a specific order.
-
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
-
keys − Key represents a value of a node based on which a search operation is to be carried out for a node.
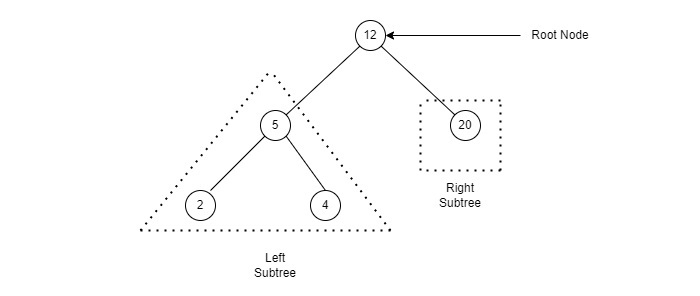
Binary Search Tree Representation
a Tree where A node’s left child must have a value less than its parent’s value and the node’s right child must have a value greater than its parent value.
The code to write a tree node would be similar to what is given below. It has a data part and references to its left and right child nodes ,also you can add a key to it.
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
In a tree, all nodes share common construct.
BST Basic Operations
The basic operations that can be performed on a binary search tree data structure, are the following −
-
Insert − Inserts an element in a tree/create a tree.
-
Search − Searches an element in a tree.
-
Preorder Traversal − Traverses a tree in a pre-order manner.
-
Inorder Traversal − Traverses a tree in an in-order manner.
-
Postorder Traversal − Traverses a tree in a post-order manner.