Spanning Tree
A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected.
By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.
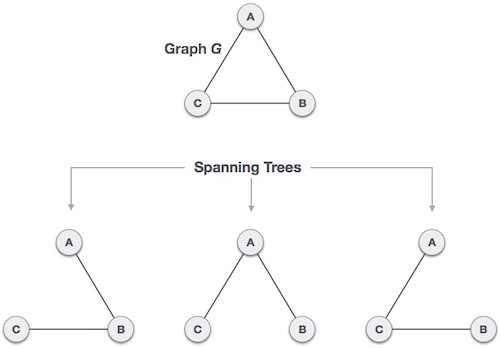
A complete undirected graph can have maximum nn-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 33−2 = 3 spanning trees are possible.
General Properties of Spanning Tree
We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −
-
A connected graph G can have more than one spanning tree.
-
All possible spanning trees of graph G, have the same number of edges and vertices.
-
The spanning tree does not have any cycle (loops).
-
Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.
-
Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.
Mathematical Properties of Spanning Tree
-
Spanning tree has n-1 edges, where n is the number of nodes (vertices).
-
From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.
A complete graph can have maximum nn-2 number of spanning trees.
Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree.
Application of Spanning Tree
Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −
- Civil Network Planning
- Computer Network Routing Protocol
- Cluster Analysis
Minimum Spanning Tree (MST)
In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.