Kruskal’s Spanning Tree Algorithm

Kruskal’s algorithm to find the minimum cost spanning tree uses the greedy approach.

This algorithm treats the graph as a forest and every node it has as an individual tree. A tree connects to another only and only if, it has the least cost among all available options and does not violate MST(Minimum Spanning Tree) properties

To understand Kruskal’s algorithm let us consider the following example

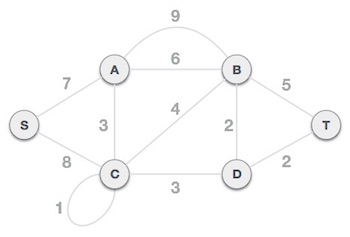
Step 1 - Remove all loops and Parallel Edges

Remove all loops and parallel edges from the given graph.

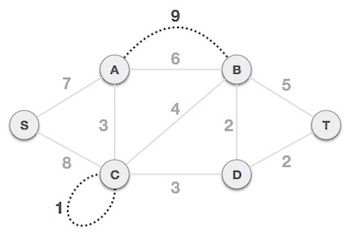
In case of parallel edges, keep the one which has the least cost associated and remove all others.

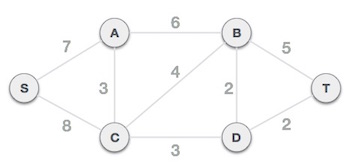
Step 2 - Arrange all edges in their increasing order of weight

The next step is to create a set of edges and weight, and arrange them in an ascending order of weightage (cost).

Step 3 - Add the edge which has the least weightage

Now we start adding edges to the graph beginning from the one which has the least weight. Throughout, we shall keep checking that the spanning properties remain intact. In case, by adding one edge, the spanning tree property does not hold then we shall consider not to include the edge in the graph.

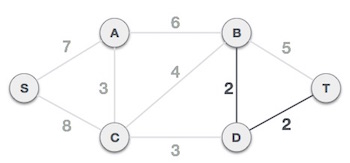
The least cost is 2 and edges involved are B,D and D,T. We add them. Adding them does not violate spanning tree properties, so we continue to our next edge selection.

Next cost is 3, and associated edges are A,C and C,D. We add them again −

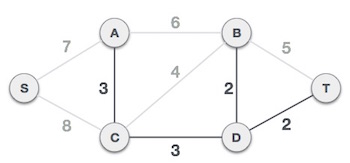
Next cost in the table is 4, and we observe that adding it will create a circuit in the graph.

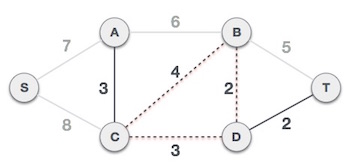
We ignore it. In the process we shall ignore/avoid all edges that create a circuit.

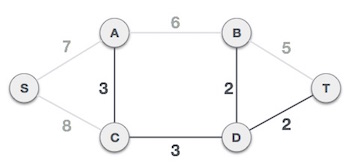
We observe that edges with cost 5 and 6 also create circuits. We ignore them and move on.

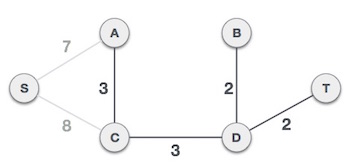
Now we are left with only one node to be added. Between the two least cost edges available 7 and 8, we shall add the edge with cost 7.

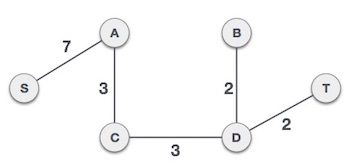
By adding edge S,A we have included all the nodes of the graph and we now have minimum cost spanning tree.